Me at Jinji Lake in Suzhou, Summer 2023 (Courtesy of Jiayi)
Hi There!
My name is Xiwei (Peter) Pan, originally from the historic city of Yangzhou , China. I am a first-year Ph.D. student at Princeton University , where I will be working with Prof. Liuchi Li . My research interests lie in multibody frictional contact, nonlinear problems, asymptotic analysis, plate and shell theories, and the application of machine learning methods to these areas.
Prior to that, I earned a master’s degree in Mechanics (advised by Prof. Yichao Zhu ) and a bachelor’s degree in Engineering Mechanics through the Qian Lingxi Excellence in Education Program, both from Dalian University of Technology (DUT) .
Beyond research, I enjoy playing (table) tennis, swimming, photography, and staying active (both physically and mentally).
News
Jul 01, 2025
My second research paper got accepted by the International Journal of Engineering Science!
Jun 11, 2025
Graduated with a master's degree from DUT and received the Outstanding Master's Thesis Award.
Dec 29, 2024
Recommended as an Outstanding Graduate of the 2025 Class at DUT and an Outstanding Graduate of the 2025 Class of Liaoning Province.
Sep 20, 2024
Rated as the Outstanding Graduate Student of DUT.
Jul 21, 2024
Attend the 16th World Congress on Computational Mechanics (WCCM 2024) @ Vancouver, Canada.
Selected Publications
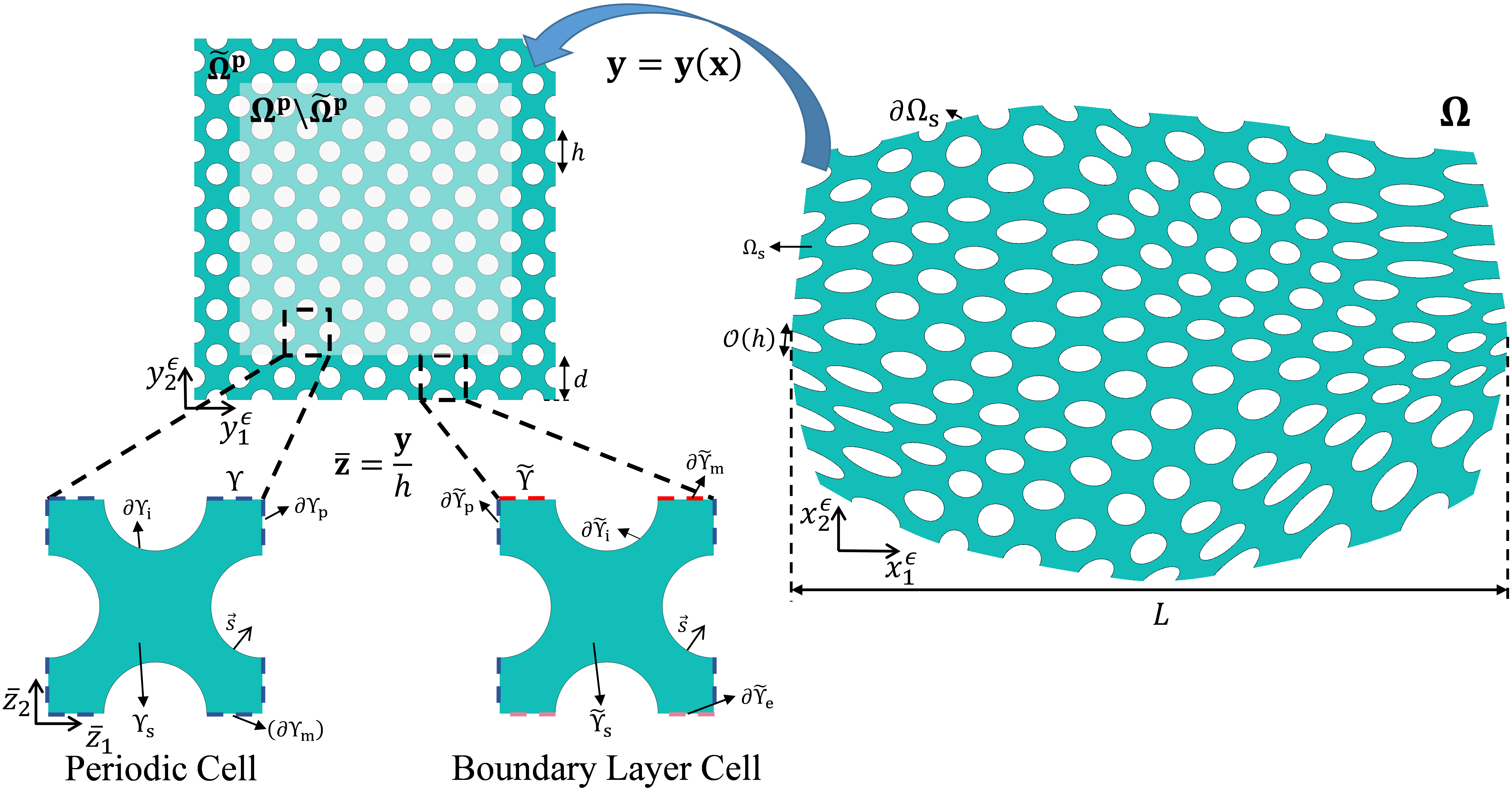
Machine-learning-based asymptotic homogenisation and localisation considering boundary layer effects
Xiwei Pan, Zhengcheng Zhou, Chuang Ma, Shaoshuai Li, and Yichao Zhu
Asymptotic homogenisation offers a way to efficiently analyse the mechanical behaviour of multiscale configurations. But near a multiscale boundary, the homogenisation strategy should be modified, as the underlying periodicity assumption breaks down there. In this article, we introduce a machine-learning-based asymptotic homogenisation and localisation scheme to formulate such boundary layer effects. To this end, we define a set of boundary layer cells, where external loading conditions are imposed on one side of the cell, and matching conditions with the interior periodic cells are imposed on the opposite side. The formulation is also extended to cover situations where the multi-scale structure is not fully periodic, but spatially varying. Implied from the asymptotic results, neural networks can be trained to memorise the interrelationship between key local quantities, such as the magnitude of the local maximum von Mises stress, and the local mechanical and geometric features. Equipped with the trained neural networks, the online calculation for key (boundary-localised) quantities of interest under arbitrary loading conditions is expected to be accelerated substantially. Numerical examples are further presented to show the reliability of the proposed work for boundary stress prediction.
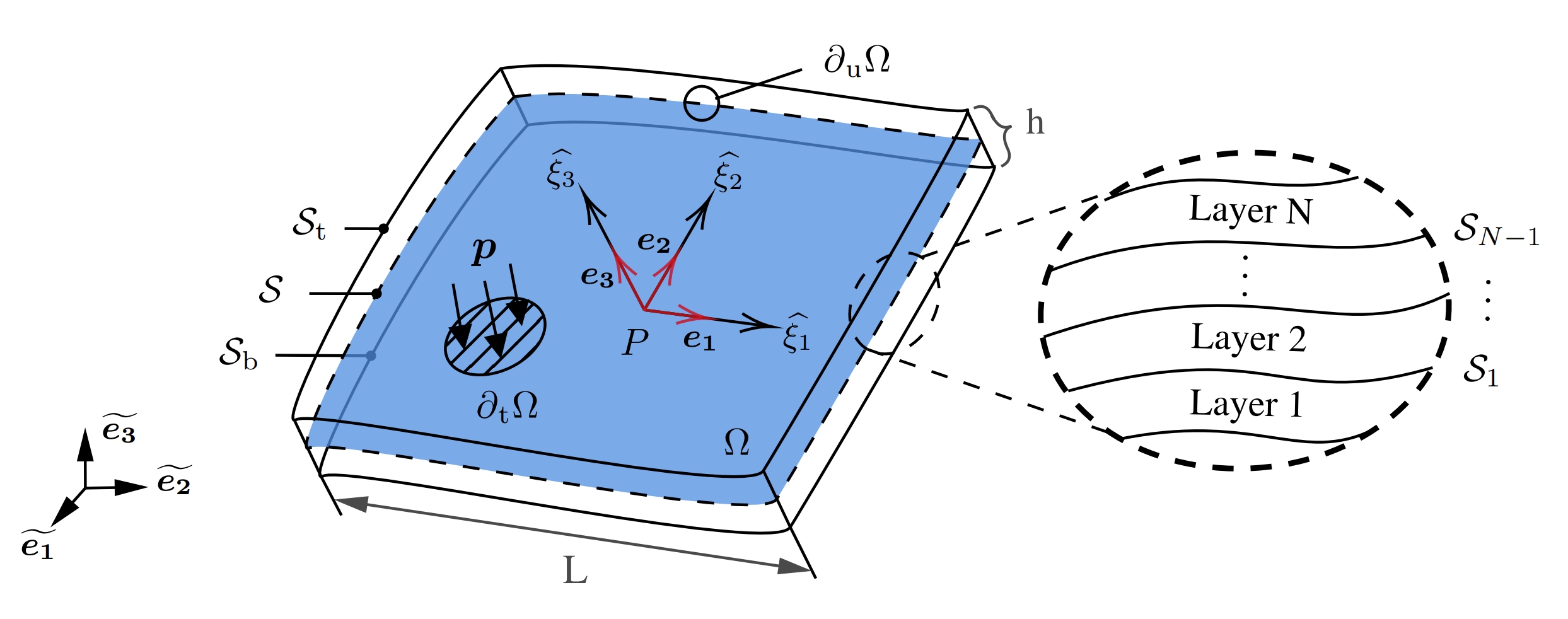
Asymptotic formulation of the role of shear loads on multi-layered thin shells and classification of their deformation modes
Xiwei Pan, Yichao Zhu
Shell structures are generally modeled based on kinematic hypotheses, where some of the parameters are preferentially evaluated in a phenomenological manner. In this article, asymptotic analysis against the underlying three-dimensional equation system is considered so as to provide a rational framework for modeling and interpreting the deformation behavior of multi-layered thin shells (MTSs). Capable of accurately predicting both overall stiffness and detailed stress distribution, the proposed shell theory shows its distinguishing features at least in the following aspects. Firstly, it naturally introduces a rule for classifying the deformation modes of MTSs based on the magnitude of the maximum dimensionless principal curvature. Secondly, for each class, the hierarchy in the order of the involved field quantities is examined, and it is shown that when the product of the maximum principal curvature and the characteristic shell size reaches the magnitude of unity or larger, the resulting shell theory cannot be treated by natural extension of plate theories. Lastly, it is demonstrated that, for moderate shear forces and comparable material properties, a leading-order multi-layered shell theory derived from asymptotic analysis should suffice to output satisfactory predictions over the shell stiffness, as well as its internal stress distribution. Numerical examples of the deformation and strength analysis for MTSs are also presented to show the reliability of the leading-order model.
